Welcome

0%

数据结构--二叉树

发表于 分类于

二叉树的定义

二叉树（Binary Tree）是 n（n >= 0）个结点的有限集合，该集合或者为空集（空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左二叉树和右二叉树组成。

注：二叉树不是树的特例，因为二叉树的孩子有左右之分，树是图的特例，二叉树可以为空，图（包括树）不能为空。（不同参考书籍的描述不一，有待考量）

二叉树特点

  • 每个结点最多有两棵子树，所以二叉树中不存在度大于 2 的结点。
  • 左子树和右子树是有顺序的，次序不能任意颠倒。
  • 即使树中某结点只有一棵子树，也要区分它是左子树还是右子树。

二叉树的五种基本形态：

  1. 空二叉树：结点个数为零的二叉树（普通树的结点个数至少为1）
  2. 只有一个根结点
  3. 根结点只有左子树
  4. 根结点只有右子树
  5. 根结点既有左子树又有右子树

特殊二叉树

  1. 斜树

所有的结点都只有左子树的二叉树叫左斜树。所有结点都是只有右子树的二叉树叫右斜树。这两者统称为斜树。

  1. 满二叉树

在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树称为满二叉树。

满二叉树的特点：

（1）叶子只能出现在最下一层。
（2）非叶子结点的度一定是2。
（3）在同样深度的二叉树中，满二叉树的结点个数最多，叶子数最多。

  1. 完全二叉树

对一棵具有 n 个结点的二叉树按层序编号，如果编号为 i (1<=i<=n) 的结点与同样深度的满二叉树中编号为 i 的结点在二叉树中位置完全相同，则这棵二叉树称为完全二叉树。

完全二叉树的特点：

（1）叶子结点只能出现在最下两层。
（2）最下层的叶子一定集中在左部连续位置。
（3）倒数二层，若有叶子结点，一定都在右部连续位置。
（4）如果结点度为1, 则该结点只有左孩子，即不存在只有右子树的情况。
（5）同样结点数的二叉树，完全二叉树的深度最小。

二叉树的性质

  1. 在二叉树的第i层上至多有$2^{i-1}$个结点(i>=1)
  2. 深度为k的二叉树至多有$2^k-1$个结点
  3. 对任何一棵二叉树T，如果其终端结点数为n0，度为2的结点数为n2，则$n_0=n_2+1$。
  4. 具有 n 个结点的完全二叉树的深度为$log_2n$向下取整然后+1。
  5. 如果对一棵有n个结点的完全二叉树的结点按层序编号，对任一结点i(1<=i<=n)有：
  • 如果 i=1，则结点 i 是二叉树的根，无双亲；如果 i>1，则其双亲是结点 i/2 向下取整。
  • 如果 2i>n，则结点 i 无左孩子（结点 i 为叶子结点）；否则其左孩子是结点 2i。
  • 如果 2i+1>n，则结点 i 无右孩子；否则其右孩子是结点 2i+1。

二叉树的存储结构

二叉树的顺序存储结构

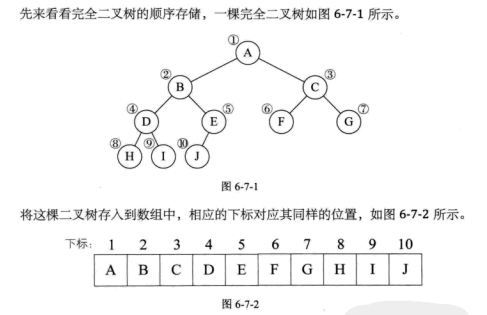
二叉树的顺序存储结构

顺序存储结构一般只用于完全二叉树。

二叉链表

二叉链表：一个数据域和两个指针域

| lchild | data | rchild |

1
2
3
4
5
6
7
8
9
10
11
12
/* 二叉树的二叉链表结点结构定义 */
template<typename T>
struct BiTNode {        // 结点结构
    T data;
    BiTNode<T> *lchild, *rchild;
    
    //无参构造函数
    BiTNode() :lchild(NULL), rchild(NULL) {}

    //带默认值的有参构造函数
    BiTNode(T mData, BiTNode<T> *l = NULL, BiTNode<T> *r = NULL) :data(mData), lchild(l), rchild(r) {}
};

结构示意图如图所示：

二叉链表

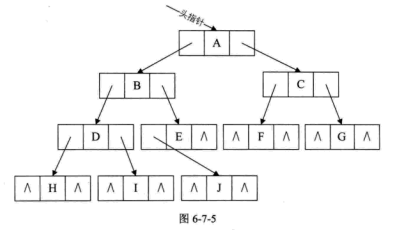
遍历二叉树

二叉树的遍历（traversing binary tree）是指从根结点出发，按照某种次序依次访问二叉树中所有结点，使得每个结点被访问一次且仅被访问一次。

1. 前序遍历

若二叉树为空，则空操作返回，否则先访问根结点，然后前序遍历左子树，再前序遍历右子树。

前序

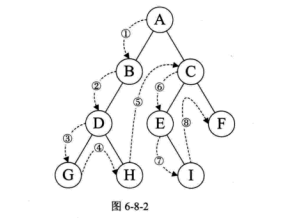
2. 中序遍历

若树为空，则空操作返回，否则从根结点开始（注意并不是先访问根结点），中序遍历根结点的左子树，然后是访问根结点，最后中序遍历右子树。

中序

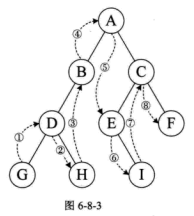
3. 后序遍历

若树为空，则空操作返回，否则从左到右先叶子后结点的方式遍历访问左右子树，最后是访问根结点。

后序

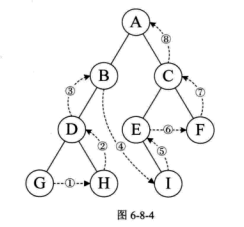
4. 层序遍历

若树为空，则空操作返回，否则从树的第一层，也就是根结点开始访问，从上而下逐层遍历，在同一层中，按从左到右的顺序对结点逐个访问。

层序

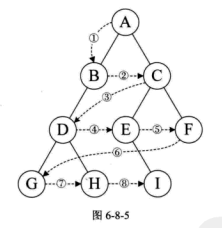
前序遍历算法

  1. 采用前序遍历的递归算法：
1
2
3
4
5
6
7
8
9
void PreOrderTraverse(BiTNode<T> *&subTree)
{
    if (subTree != NULL)
    {
        cout << subTree->data << endl;
        PreOrderTraverse(subTree->lchild);
        PreOrderTraverse(subTree->rchild);
    }
}
  1. 前序遍历的非递归算法：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
void PreOrderTraverser_NoRecursion(BiTNode<T> *&root)
{
    if (root == NULL)
    {
        return;
    }
    stack<BiTNode<T> *> s;
    BiTNode<T> *t;
    s.push(root);        //根结点进栈
    while (!s.empty())
    {
        t = s.top();
        s.pop();
        cout << t->data << endl;
        if (t->rchild != NULL)        //后进栈的先弹出（LIFO）
        {
            s.push(t->rchild);
        }
        if (t->lchild != NULL)
        {
            s.push(t->lchild);
        }
    }
}

中序遍历算法

中序遍历的递归算法：

1
2
3
4
5
6
7
8
9
void InOrderTraverse(BiTNode<T> *&subTree)
{
    if (subTree != NULL)
    {
        InOrderTraverse(subTree->lchild);
        cout << subTree->data << endl;
        InOrderTraverse(subTree->rchild);
    }
}

后序遍历算法

后序遍历的递归算法：

1
2
3
4
5
6
7
8
9
void PostOrderTraverse(BiTNode<T> *&subTree)
{
    if (subTree != NULL)
    {
        PostOrderTraverse(subTree->lchild);
        PostOrderTraverse(subTree->rchild);
        cout << subTree->data << endl;
    }
}

层级遍历算法

层级遍历的非递归算法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void LevelOrderTraverse_NoRecursion(BiTNode<T> *&root)
{
    if (root == NULL)
    {
        return;
    }
    queue<BiTNode<T> *> q;
    BiTNode<T> *t;
    q.push(root);
    while (!q.empty())
    {
        t = q.front();
        q.pop();
        cout << t->data << endl;
        if (t->lchild != NULL)        //先进队列的先弹出（FIFO）
        {
            q.push(t->lchild);
        }
        if (t->rchild != NULL)
        {
            q.push(t->rchild);
        }
    }

}

线索二叉树

指向前驱结点和后继结点的指针称为线索，加上线索的二叉链表称为线索链表，相应的二叉树就称为线索二叉树。
对二叉树以某种次序遍历使其变为线索二叉树的过程称做是线索化。
线索化的过程就是在遍历的过程中修改空指针的过程。

线索二叉树的结点结构：
| lchild | ltag | data | rtag | rchild |

其中：

  • ltag 为 0 时指向该结点的左孩子，为 1 时指向该结点的前驱。
  • rtag 为 0 时指向该结点的右孩子，为 1 时指向该结点的后继。

如果所用的二叉树需经常遍历或査找结点时需要某种遍历序列中的前驱和后继，那么采用线索二叉链表的存储结构就是非常不错的选择。

树、森林与二叉树的转换

树转换成二叉树

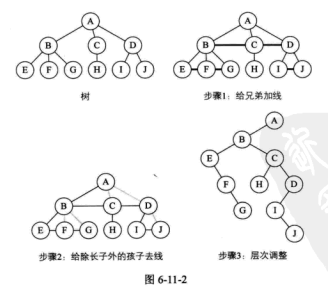
转换步骤如下：

  1. 加线。在所有兄弟结点之间加一条连线。
  2. 去线。对树中每个结点，只保留它与第一个孩子结点的连线，删除它与其他孩子结点之间的连线。（叶子节点没有孩子结点，不用去线）
  3. 层次调整。以树的根结点为轴心，将整棵树顺时针旋转一定的角度，使之结构层次分明。注意第一个孩子是二叉树结点的左孩子，兄弟转换过来的孩子是结点的右孩子。

树转换成二叉树

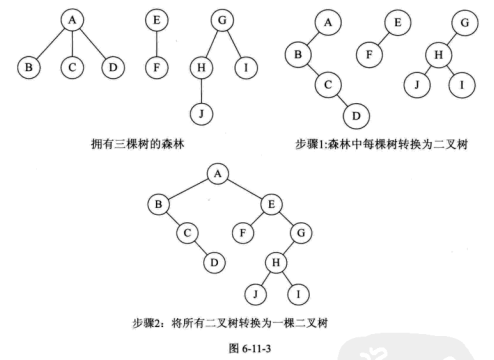
森林转换成二叉树

森林是由若干棵树组成的，所以完全可以理解为，森林中的每一棵树都是兄弟，可以按照兄弟的处理办法来操作。

  1. 把每一棵树转换成二叉树
  2. 第一棵二叉树不动，从第二棵二叉树开始，依次把后一棵二叉树的根结点作为前一棵二叉树的根结点的右孩子，用线连接起来。当所有的二叉树连接起来后就得到了由森林转换来的二叉树。

森林转换成二叉树

树与森林的遍历

树的遍历分为两种方式：

  1. 先根遍历树：先访问树的根节点，然后依次先根遍历每棵子树（前序遍历）
  2. 后根遍历树：先依次后根遍历每棵子树，然后再访问根节点（中序遍历）

森林的遍历也分为两种方式：

  1. 前序遍历：先访问森林中第一棵树的根结点，然后再依次先根遍历根的每棵子树，再依次用同样方式遍历除去第一棵树的剩余树构成的森林。
  2. 后序遍历：是先访问森林中第一棵树，后根遍历的方式遍历每棵子树，然后再访问根结点，再依次同样方式遍历除去第一棵树的剩余树构成的森林。

赫夫曼树及应用

赫夫曼树

从树中一个结点到另一个结点之间的分支构成两个结点之间的路径，路径上的分支数目称做路径长度。树的路径长度就是从树根到每一结点的路径长度之和。
如果考虑到带权的结点，结点的带权的路径长度为从该结点到树根之间的路径长度与结点上权的乘积。树的带权路径长度为树中所有叶子结点的带权路径长度之和。
带权路径长度最小的二叉树称做赫夫曼树。

构造赫夫曼树的赫夫曼算法描述：

  1. 根据给定的 n 个权值$\{w_1, w_2, … ,w_n\}$构成 n 棵二叉树的集合$F=\{T_1, T_2, … ,T_n\}$，其中每棵二叉树$T_i$中只有一个带权为$w_i$根结点，其左右子树均为空。
  2. 在 F 中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树，且置新的二叉树的根结点的权值为其左右子树上根结点的权值之和。
  3. 在 F 中删除这两棵树，同时将新得到的二叉树加入 F 中。
  4. 重复 2 和 3 步骤，直到 F 只含一棵树为止。这棵树便是赫夫曼树。

赫夫曼编码

一般地，设需要编码的字符集为$\{d_1, d_2, … ,d_n\}$，各个字符在电文中出现的次数或频率集合为$\{w_1, w_2, … ,w_n\}$，以${d_1, d_2, … ,d_n}$为叶子结点，${w_1, w_2, … ,w_n}$作为相应叶子结点的权值来构造一棵赫夫曼树。规定赫夫曼树的左分支代表 0，右分支代表 1，则从根结点到叶子结点所经过的路径分支组成的 0 和 1 的序列便为该结点对应字符的编码，这就是赫夫曼编码。