数据结构--图

图的定义

图（Graph）是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G(V,E)，其中，G 表示一个图，V 是图 G 中顶点的集合，E 是图 G 中边的集合。

注意：

• 线性表中我们把数据元素叫元素，树中将数据元素叫结点，在图中数据元素，我们则称之为顶点（Vertex）。
• 线性表中可以没有数据元素，称为空表。树中可以没有结点，叫做空树。在图结构中，不允许没有顶点。在定义中，若 V 是顶点的集合，则强调了顶点集合 V 有穷非空（关于点集是否为空有争议）。

• 线性表中，相邻的数据元素之间具有线性关系，树结构中，相邻两层的结点具有层次关系，而图中，任意两个顶点之间都可能有关系，顶点之间的逻辑关系用边来表示，边集可以是空的。

无向图：图中任意两个顶点之间的边都是无向边（顶点之间的边没有方向，用无序偶对($v_i, v_j$)表示）。
有向图：图中任意两个顶点之间的边都是有向边（从顶点$v_i$ 到 $v_j$的边有方向，用有序偶对\<$v_i, v_j$>来表示，也称为弧，$v_i$为弧尾，$v_j$为弧头）。
简单图：图中不存在顶点到其自身的边，且一条边不重复出现的图。
无向完全图：无向图中任意两个顶点之间都存在边的图。
有向完全图：有向图中任意两个顶点之间都存在方向互为相反的两条弧的图。
稀疏图：有很少条边或者弧的图，反之称为稠密图。
网（Network）：带权（weight，与图的边或者弧相关的数）的图

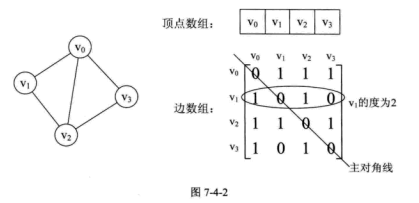
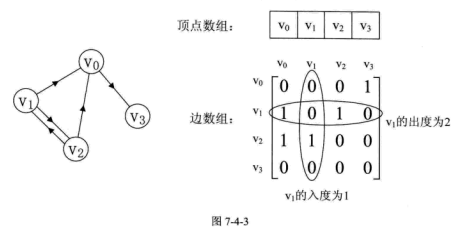
对于无向图，顶点v的度是和该顶点相关联的边的数目，记为TD(v)；
无向图的边数是各顶点度数和的一半。
对于有向图，以顶点v为头的弧的数目称为v的入度，记为ID(v)；以v为尾的弧的数目称为v的出度，记为OD(v)；
有向图的弧条数等于各顶点的出度和等于各顶点的入度和。

路径的长度是路径上的边或弧的数目。
第一个顶点到最后一个顶点相同的路径称为回路或环（Cycle）。序列中顶点不重复出现的路径称为简单路径。除了第一个顶点和最后一个顶点之外，其余顶点不重复出现的回路，称为简单回路或简单环。

在无向图 G 中，如果从顶点$v_i$到顶点$v_j$有路径，则称$v_i$和$v_j$是连通的。如果对于
图中任意两个顶点 $v_i, v_j∈E$，$v_i$和$v_j$都是连通的，则称 G 是连通图。
无向图中的极大连通子图称为连通分量。它强调：

• 要是子图；
• 子图要是联通的；
• 连通子图含有极大顶点数；
• 具有极大顶点数的连通子图包含依附于这些顶点的所有边。

在有向图 G 中，如果对于每一对的$v_i, v_j∈V$、$v_i ≠ v_j$，从$v_i$和$v_j$和从$v_j$和$v_i$都存在路径，则称 G 是强连通图。有向图中的极大强连通子图称做有向图的强连通分量。

一个连通图的生成树是一个极小的连通子图，它含有图中全部的 n 个顶点，但只有足以构成一棵树的 n-1 条边。
如果一个有向图恰有一个顶点的入度为0, 其余顶点的入度均为 1, 则是一棵有向树。
一个有向图的生成森林由若干棵有向树组成，含有图中全部顶点，但只有足以构成若干棵不相交的有向树的弧。

图的存储结构

邻接矩阵

图的邻接矩阵（Adjacency Matrix）存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组（称为邻接矩阵）存储图中的边或弧的信息。

缺点：对于边数相对顶点较少的图，对存储空间有较大浪费。

#define MAX_VEX        100        // 最大顶点数

//邻接矩阵
template<typename VertexType, typename EdgeType>
struct AMGraph {
    VertexType vexs[MAX_VEX];        // 顶点表
    EdgeType arc[MAX_VEX][MAX_VEX];    // 邻接矩阵，可看做边表
    int num_vertexes, num_edges;        // 图中当前的顶点数和边数
};

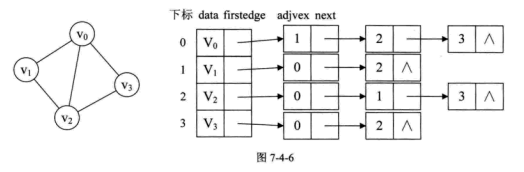
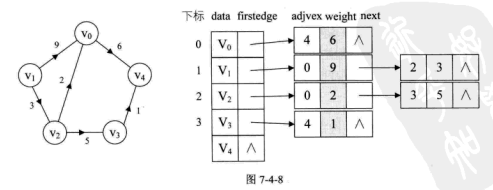
邻接表

对边或弧使用链式存储的方式来避免空间浪费的问题，这种数组与链表相结合的存储方法称为邻接表。
图中每个顶点$v_i$的所有邻接点构成一个线性表，由于邻接点的个数不定，所以用单链表存储，无向图称为顶点$v_i$的边表，有向图则称为顶点$v_i$作为弧尾的出边表。

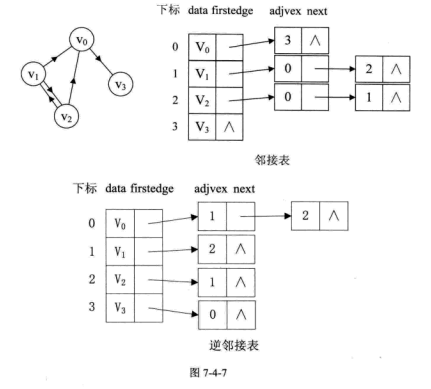
有向图的逆邻接表：对每个顶点$v_i$都建立一个链接为$v_i$为弧头的表.

对于带权值的网图，可以在边表结点定义中再增加一个 weight 的数据域，存储权值信息即可。

//邻接表
template<typename EdgeType>
struct EdgeNode {
    int adjvex;
    EdgeType weight;
    EdgeNode *next;
};

template<typename VertexType, typename EdgeType>
struct VertexNode {
    VertexType data;
    EdgeNode<EdgeType> *firstedge;
};

//该结构体是上两个结构体的整合
template<typename VertexType, typename EdgeType>
struct ALGraph {
    VertexNode<VertexType, EdgeType> adj_list[MAX_VEX];
    int num_vertexes, num_edges;
};

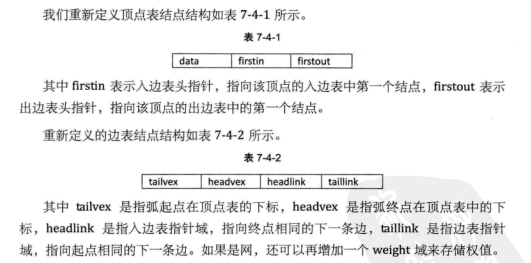
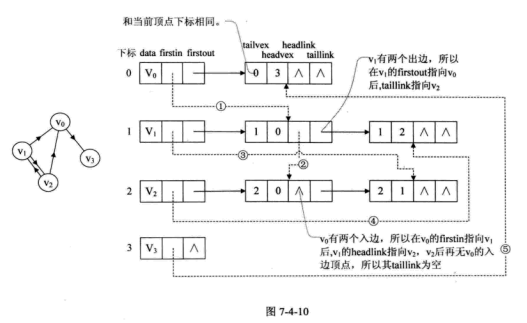
十字链表

十字链表：把邻接表与逆邻接表结合起来的存储方法。

十字链表的好处就是因为把邻接表和逆邻接表整合在了一起，这样既容易找到以$v_i$为尾的弧，也容易找到以$v_i$为头的弧，因而容易求得顶点的出度和入度。而且它除了结构复杂一点外，其实创建图算法的时间复杂度是和邻接表相同的，因此，在有向图的应用中，十字链表是非常好的数据结构模型。

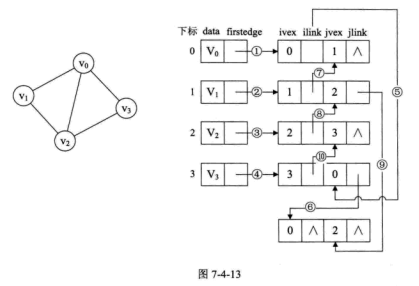
邻接多重表

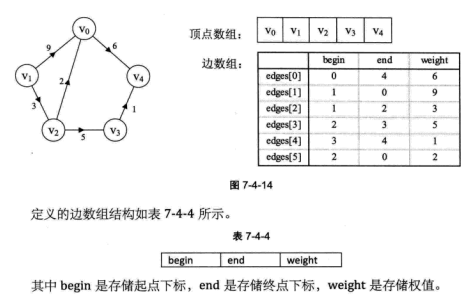
边集数组

边集数组是由两个一维数组构成。一个是存储顶点的信息；另一个是存储边的信息，这个边数组毎个数据元素由一条边的起点下标（begin）终点下标（end）和权（weight）组成。

边集数组关注的是边的集合，在边集数组中要查找一个顶点的度需要扫描整个边数组，效率并不高。因此它更适合对边依次进行处理的操作，而不适合对顶点相关的操作。

图的遍历

从图中某一顶点出发访遍图中其余顶点，且使每一个顶点仅被访问一次，这一过程就叫做图的遍历 (Traversing Graph)。

深度优先遍历

深度优先遍历 (Depth_First_Search)，也称为深度优先搜索，简称为 DFS 。
深度优先遍历其实就是一个递归的过程，也是一棵树的前序遍历过程。它从图中某个顶点 v 出发，访问此顶点，然后从 v 的未被访问的邻接点出发深度优先遍历图，直至图中所有和 v 有路径相通的顶点都被访问到。事实上，我们这里讲到的是连通图，对于非连通图，只需要对它的连通分量分别进行深度优先遍历，即在先前一个顶点进行一次深度优先遍历后，若图中尚有顶点未被访问，则另选图中一个未曾被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。

//指示访问标志
bool visited_[MAX_VEX];

//邻接矩阵的深度优先遍历
void DFS(AMGraph<VertexType, EdgeType> *&am_graph, int i) {
    int j;
    visited_[i] = true;
    cout << am_graph->vexs[i] << endl;
    for (j = 0; j < am_graph->num_vertexes; j++) {
        if (am_graph->arc[i][j] == 1 && !visited_[j]) {  //对未访问的邻接节点递归调用
            DFS(am_graph, j);
        }
    }
}

void DFSTraverse(AMGraph<VertexType, EdgeType> *&am_graph) {
    int i;
    for (i = 0; i < am_graph->num_vertexes; i ++) {
        visited_[i] = false;
    }
    for (i = 0; i < am_graph->num_vertexes; i++) {
        if (!visited_[i]) {  //对未访问过的节点调用DFS，若是连通图，则只会调用一次
            DFS(am_graph, i);
        }
    }
}

//邻接表的深度优先遍历
void DFS(ALGraph<VertexType, EdgeType> *&al_graph, int i) {
    EdgeNode<EdgeType> *edge;
    visited_[i] = true;
    cout << al_graph->vexs[i] << endl;
    edge = al_graph->adj_list[i].firstedge;
    while (edge) {
        if (!visited[edge->adjvex]) {  //对未访问的邻接节点递归调用
            DFS(al_graph, edge->adjvex);
        }
        edge = edge->next;
    }
}

void DFSTraverse(ALGraph<VertexType, EdgeType> *&al_graph) {
    int i;
    for (i = 0; i < al_graph->num_vertexes; i++) {
        visited_[i] = false;
    }
    for (i = 0; i < al_graph->num_vertexes; i++) {
        if (!visited_[i]) {  //对未访问过的节点调用DFS，若是连通图，则只会调用一次
            DFS(al_graph, i);
        }
    }
}

对比两个不同存储结构的深度优先遍历算法，对于 n 个顶点 e 条边的图来说，邻接矩阵由于是二维数组，要查找每个顶点的邻接点需要访问矩阵中的所有元素，因此都需要$O(n^2)$的时间。而邻接表做存储结构时，找邻接点所需的时间取决于顶点和边的数量，所以是$O(n+e)$显然对于点多边少的稀疏图来说，邻接表结构使得算法在时间效率上大大提高。

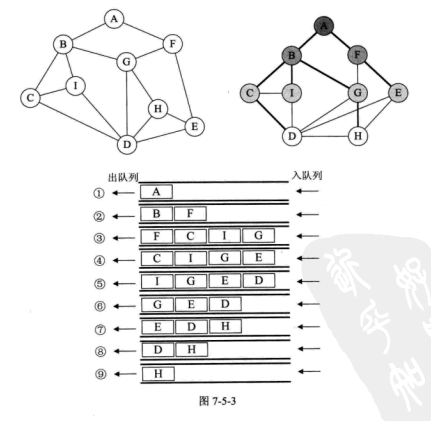
广度优先遍历

广度优先遍历 (Breadth_First_Search)，又称为广度优先搜索，简称 BFS 。
如果说图的深度优先遍历类似树的前序遍历，那么图的广度优先遍历就类似于树的层序遍历。层序遍历之前需要将图稍微变形，变形原则是顶点 A 放置在最上第一层，让与它有边的顶点 B、F 为第二层，再让与 B 和 F 有边的顶点 C、I、G、E 为第三层，再将这四个顶点有边的 D、H 放在第四层。

/*
    邻接矩阵的广度遍历算法
*/
void BFSTraverseAM(AMGraph<VertexType, EdgeType> *&am_graph) {
    using namespace std;

    int i, j;
    queue<int> vertex_queue;
    for (i = 0; i < am_graph->num_vertexes; i++) {
        visited[i] = false;
    }
    for (i = 0; i < am_graph->num_vertexes; i++) {
        if (!visited[i]) {
            visited[i] = true;
            cout << am_graph->vexs[i] << endl;
            vertex_queue.push(i);  //顶点index入队列
            while (!vertex_queue.empty()) {  //若当前队列不为空
                i = vertex_queue.front();  //返回当前队列首元素
                vertex_queue.pop();
                for (j = 0; j < am_graph->num_vertexes; j++) {
                    if (am_graph->arc[i][j] == 1 && !visited[j]) {
                        visited[j] = true;
                        cout << am_graph->vexs[j] << endl;
                        vertex_queue.push(j);
                    }
                }
            }
        }
    }
}

/*
邻接表的广度遍历算法
*/
void BFSTraverseAL(ALGraph<VertexType, EdgeType> *&al_graph) {
    using namespace std;

    int i;
    queue<int> vertex_queue;
    EdgeNode<EdgeType> *edge;
    for (i = 0; i < al_graph->num_vertexes; i++) {
        visited_[i] = false;
    }
    for (i = 0; i < al_graph->num_vertexes; i++) {
        if (!visited_[i]) {
            visited_[i] = true;
            cout << al_graph->adj_list[i].data << endl;
            vertex_queue.push(i);  //顶点index入队列
            while (!vertex_queue.empty()) {  //若当前队列不为空
                i = vertex_queue.front();  //返回当前队列首元素
                vertex_queue.pop();
                edge = al_graph->adj_list[i].firstedge;
                while (edge) {
                    if (!visited_[edge->adjvex]) {  //若该节点未被访问
                        visited_[edge->adjvex] = true;
                        cout << al_graph->adj_list[edge->adjvex].data << endl;
                        vertex_queue.push(edge->adjvex);
                    }
                    edge = edge->next;
                }
            }
        }
    }
}

图的深度优先遍历与广度优先遍历算法在时间复杂度上是一样的，不同之处仅仅在于对顶点访问的顺序不同。深度优先更适合目标比较明确，以找到目标为主要目的的情况，而广度优先更适合在不断扩大遍历范围时找到相对最优解的情况。

最小生成树

我们把构造连通网的最小代价生成树称为最小生成树 (Minimum Cost Spanning Tree)。

普里姆 (Prim) 算法

普里姆 (Prim) 算法是以某顶点为起点，逐步找各顶点上最小权值的边来构建最小生成树。
构造邻接矩阵：

/*
  最小生成树 Prim 算法的定义
  核心思想：遍历顶点，由顶点找最小权值对应的边
  图示例：9 15 012345678 0 1 10 0 5 11 1 2 18 1 6 16 1 8 12 2 3 22 2 8 8 3 4 20 3 6 24 3 7 16 3 8 21 4 5 26 4 7 7 5 6 17 6 7 19

*/
template<typename VertexType, typename EdgeType>
void Graph<VertexType, EdgeType>::MiniSpanTreePrim(AMGraph<VertexType, EdgeType> *&am_graph) {
    using namespace std;

    int min, i, j, k;
    //adjvex保存相关顶点下标；lowcost保存相关顶点间 边的权值
    vector<int> adjvex, lowcost;
    lowcost.push_back(0);
    adjvex.push_back(0);  //初始化第一个顶点为v0
    for (i = 1; i < am_graph->num_vertexes; i++) {
        lowcost.push_back(am_graph->arc[0][i]);
        adjvex.push_back(0);
    }
    for (i = 1; i < am_graph->num_vertexes; i++) {
        min = MY_INFINITY;
        j = 1; k = 0;
        while (j < am_graph->num_vertexes) {  //遍历结点，查找最小权值 
            if (lowcost[j] != 0 && lowcost[j] < min) {
                min = lowcost[j];
                k = j;
            }
            ++j;
        }
        cout << "(" << adjvex[k] << "," << k << ") ";
        lowcost[k] = 0;  //当前顶点的权值置为0
        for (j = 1; j < am_graph->num_vertexes; j++) {  //“合并”顶点
            if (lowcost[j] != 0 && am_graph->arc[k][j] < lowcost[j]) {
                lowcost[j] = am_graph->arc[k][j];
                adjvex[j] = k;
            }
        }
    }
}

由算法代码中的循环嵌套可得知此算法的时间复杂度为$O(n^2)$。

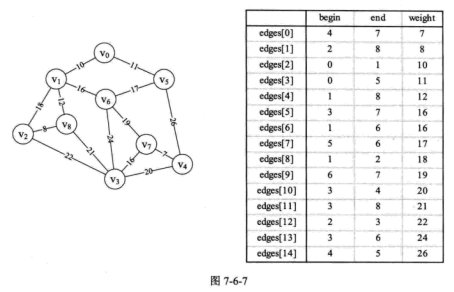
克鲁斯卡尔 (Kruskal) 算法

克鲁斯卡尔算法将各边按照权值大小排序，由小到大逐步连接顶点来构造最小生成树。
以下是 edge 边集数组结构的定义代码：

template<typename EdgeType>
struct KruskalEdge {
    int begin;
    int end;
    EdgeType weight;
};

将邻接矩阵转换成边集数组，并按照权值大小排序：

/*
最小生成树 Kruskal 算法的定义
核心思想：边按照权值排序，由最小权值的边找对应顶点
图示例：9 15 012345678 0 1 10 0 5 11 1 2 18 1 6 16 1 8 12 2 3 22 2 8 8 3 4 20 3 6 24 3 7 16 3 8 21 4 5 26 4 7 7 5 6 17 6 7 19

*/
template<typename VertexType, typename EdgeType>
void Graph<VertexType, EdgeType>::MiniSpanTreeKruskal(AMGraph<VertexType, EdgeType> *&am_graph) {
    using namespace std;

    int i, j, n, m;
    vector<KruskalEdge<EdgeType>> edges;  //边集数组
    vector<int> parent(am_graph->num_vertexes, 0);
    KruskalEdge<EdgeType> kruskal_edge;
    for (i = 0; i < am_graph->num_vertexes; i++) {  //边集数组初始化
        for (j = i+1; j < am_graph->num_vertexes; j++) {
            if (am_graph->arc[i][j] != MY_INFINITY) {
                kruskal_edge.begin = i;
                kruskal_edge.end = j;
                kruskal_edge.weight = am_graph->arc[i][j];
                edges.push_back(kruskal_edge);
            }
        }
    }
    sort(edges.begin(), edges.end(), CompareWeight);  //边集数组按照权值由小到大排序
    for (i = 0; i < am_graph->num_edges; i++) {
        n = FindIndex(parent, edges[i].begin);
        m = FindIndex(parent, edges[i].end);
        if (n != m) {  //假如 n 与 m 不等，说明此边没有与现有生成树形成环路
            parent[n] = m;  //将此边的结尾顶点放入下标为起点的 parent 中，表示此頂点已经在生成树集合中
            cout << "(" << edges[i].begin << "," << edges[i].end << ") " << edges[i].weight << endl;
        }
    }
}

/*
    权值按照由小到大的排序规则
*/
static bool CompareWeight(const KruskalEdge<EdgeType> &first, const KruskalEdge<EdgeType> &second) {
    return first.weight < second.weight;
}
    
/*
    查找连线顶点的尾部下标
*/
int FindIndex(std::vector<int> &parent, int f) {
    while (parent[f] > 0) {
        f = parent[f];
    }
    return f;
}

此算法的 FindIndex 函数由边数 edges 决定，时间复杂度为$O(logn)$，而外面有一个 for 循环 e 次。所以克鲁斯卡尔算法的时间复杂度为$O(nlogn)$。
对比两个算法，克鲁斯卡尔算法主要是针对边来展开，边数少时效率会非常高，所以对于稀疏图有很大的优势；而普里姆算法对于稠密图，即边数非常多的情况会更好一些。

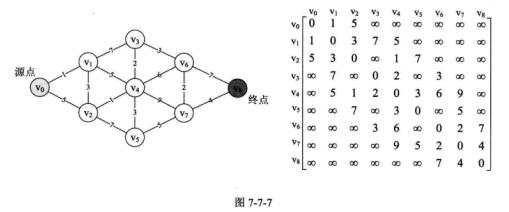
最短路径

对于网图来说，最短路径，是指两顶点之间经过的边上权值之和最少的路径，并且我们称路径上的第—个顶点是源点，最后一个顶点是终点。

迪杰斯特拉 (Dijkstra) 算法

这是一个按路径长度递增的次序产生最短路径的算法。该算法一步步求出源点和终点之间顶点的最短路径，过程中都是基于已经求出的最短路径的基础上，求得更远顶点的最短路径，最终得到源点到终点的最短路径。
示例图如下所示：

std::vector<int> path_matrix_, short_path_table_;  //存储最短路径下标，到各点最短路径的权值和

/*
最短路径 Dijkstra 算法的定义
核心思想：按路径长度递增的次序迭代（以前一次产生结果为基础）产生最短路径
图示例：9 16 012345678 0 1 1 0 2 5 1 2 3 1 3 7 1 4 5 2 4 1 2 5 7 3 4 2 3 6 3 4 5 3 4 6 6 4 7 9 5 7 5 6 7 2 6 8 7 7 8 4

*/
template<typename VertexType, typename EdgeType>
void Graph<VertexType, EdgeType>::ShortestPathDijkstra(AMGraph<VertexType, EdgeType> *&am_graph, int v0, std::vector<int> &path_matrix, std::vector<int> &short_path_table) {
    using namespace std;

    int v, w, k, min;
    vector<int> final_short_path(am_graph->num_vertexes, 0);  //final_short_path[w]=1 表示求得顶点v0到vw的最短路径
    for (v = 0; v < am_graph->num_vertexes; v++) {  //数据初始化
        path_matrix.push_back(0);
        short_path_table.push_back(am_graph->arc[v0][v]);
    }
    short_path_table[v0] = 0;  //v0到本身的路径为0
    final_short_path[v0] = 1;  //v0到本身不需要求路径
    for (v = 1; v < am_graph->num_vertexes; v++) {
        min = MY_INFINITY;
        for (w = 0; w < am_graph->num_vertexes; w++) {  //查找距离当前顶点最近的顶点k
            if (final_short_path[w] == 0 && short_path_table[w] < min) {  //w顶点离v0顶点更近
                k = w;
                min = short_path_table[w];
            }
        }
        final_short_path[k] = 1;  //将目前找到的最近的顶点置为1
        for (w = 0; w < am_graph->num_vertexes; w++) {
            if (final_short_path[w] == 0 && (min + am_graph->arc[k][w] < short_path_table[w])) {  //经过k顶点的路径比现在这条路径短
                path_matrix[w] = k;
                short_path_table[w] = min + am_graph->arc[k][w];
            }
        }
    }
}

迪杰斯特拉 (Dijkstra) 算法解决了从某个源点到其余各顶点的最短路径问题。从循环嵌套可以很容易得到此算法的时间复杂度为$O(n^2)$。
如果我们还需要知道如 v3 到 v5，v1 到 v7 这样的任一顶点到其余所有顶点的最短路径怎么办呢？此时简单的办法就是对每个顶点当作源点运行一次迪杰斯特拉 (Dijkstra) 算法，等于在原有算法的基础上，再来一次循环，此时整个算法的时间复杂度就成了$O(n^3)$。

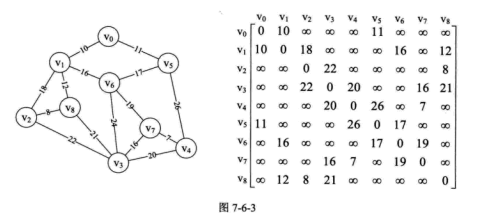
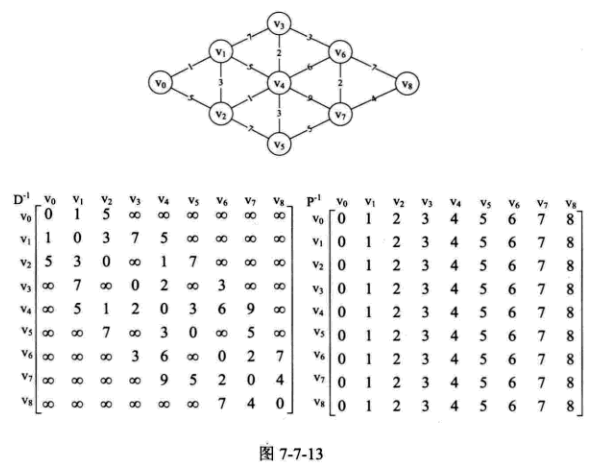
弗洛伊德 (Floyd) 算法

示例如图所示：

std::vector<std::vector<int>> floyd_path_matrix_, floyd_short_path_;  //存储最短路径的中转顶点下标，到各点最短路径的权值和

/*
最短路径 Floyd 算法的定义
核心思想：迭代（以前一次寻找结果为基础）寻找顶点与顶点间的最短中转路径
图示例：9 16 012345678 0 1 1 0 2 5 1 2 3 1 3 7 1 4 5 2 4 1 2 5 7 3 4 2 3 6 3 4 5 3 4 6 6 4 7 9 5 7 5 6 7 2 6 8 7 7 8 4

*/
template<typename VertexType, typename EdgeType>
void Graph<VertexType, EdgeType>::ShortestPathFloyd(AMGraph<VertexType, EdgeType> *&am_graph, std::vector<std::vector<int>> &floyd_path_matrix, std::vector<std::vector<int>> &floyd_short_path) {
    using namespace std;

    int v, w, k;
    // 二维数组初始化
    floyd_path_matrix.resize(am_graph->num_vertexes);
    floyd_short_path.resize(am_graph->num_vertexes);
    for (v = 0; v < am_graph->num_vertexes; v++) {
        floyd_path_matrix[v].resize(am_graph->num_vertexes);
        floyd_short_path[v].resize(am_graph->num_vertexes);
    }
    for (v = 0; v < am_graph->num_vertexes; v++) {
        for (w = 0; w < am_graph->num_vertexes; w++) {
            floyd_short_path[v][w] = am_graph->arc[v][w];
            floyd_path_matrix[v][w] = w;
        }
    }
    //k 代表的是中转顶点的下标。v 代表起始顶点，w代表结束顶点。
    for (k = 0; k < am_graph->num_vertexes; k++) {
        for (v = 0; v < am_graph->num_vertexes; v++) {
            for (w = 0; w < am_graph->num_vertexes; w++) {
                if (floyd_short_path[v][w] > floyd_short_path[k][v] + floyd_short_path[k][w]) {  //通过顶点k中转的路径小于当前路径
                    floyd_short_path[v][w] = floyd_short_path[k][v] + floyd_short_path[k][w];
                    floyd_path_matrix[v][w] = floyd_path_matrix[v][k];
                }
            }
        }
    }
}

弗洛伊德 (Floyd) 算法，它的代码简洁到就是一个二重循环初始化加一个三重循环权值修正，就完成了所有顶点到所有顶点的最短路径计算。如此简单的实现，真是巧妙之极。很可惜由于它的三重循
环，因此也是$O(n^3)$时间复杂度。如果你面临需要求所有顶点至所有顶点的最短路径问题时，弗洛伊德算法应该是不错的选择。

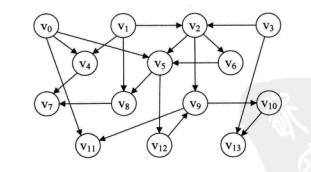
拓扑排序

在一个表示工程的有向图中，用顶点表示活动，用弧表示活动之间的优先关系，这样的有向图为顶点表示活动的网，我们称为 AOV 网 (Activity On Vertex Network)。
设 G=(V,E)是一个具有 n 个顶点的有向图，V 中的顶点序列 v1, v2, ⋯ , vn，满足若从顶点的到 vi 到 vj 有一条路径，则在顶点序列中顶点的必在顶点 vi 之前。则我们称这样的顶点序列为一个拓扑序列。拓扑排序，其实就是对一个有向图构造拓扑序列的过程。
对 AOV 网进行拓扑排序的基本思路是：从 AOV 网中选择一个入度为 0 的顶点输出，然后删去此顶点，并删除以此顶点为尾的弧，继续重复此步骤，直到输出全部顶点或者 AOV 网中不存在入度为 0 的顶点为止。考虑到算法过程中始终要查找入度为 0 的顶点，我们在原来顶点表结点结构中，增加一个入度域 in，结构如下：

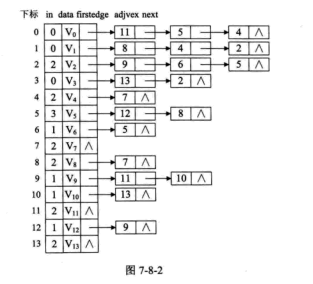
template<typename VertexType, typename EdgeType>
struct VertexNode {
    int in;                            //顶点入度
    VertexType data;                //顶点域，存储顶点信息
    EdgeNode<EdgeType> *firstedge;    //边表头栺针
};

示例有向图如下：

/*
拓扑排序的定义
函数功能：若网图无回路，输出拓扑排序序列并返回true，若有回路则返回false
*/
template<typename VertexType, typename EdgeType>
bool Graph<VertexType, EdgeType>::TopologicalSort(ALGraph<VertexType, EdgeType> *&al_graph) {
    using namespace std;

    int i, k, get_top;
    int count = 0;  //用于栈指针下标；统计输出顶点的个数
    EdgeNode<EdgeType> *edge;
    stack<int> vertex_stack;  //存储处理过程中入度为 0 的顶点，目的是为了避免每个查找时都要去遍历顶点表找有没有入度为0的顶点。
    for (i = 0; i < al_graph->num_vertexes; i++) {  //初始化填充入度数字段
        for (edge = al_graph->adj_list[i].firstedge; edge; edge = edge->next) {  //遍历该顶点对应的边表
            al_graph->adj_list[edge->adjvex].in++;
        }
    }
    for (i = 0; i < al_graph->num_vertexes; i++) {  //当前入度为零的顶点入栈
        if (al_graph->adj_list[i].in == 0) {
            vertex_stack.push(i);
        }
    }
    while (!vertex_stack.empty()) {
        get_top = vertex_stack.top();
        vertex_stack.pop();
        cout << al_graph->adj_list[get_top].data << " -> ";
        ++count;
        for (edge = al_graph->adj_list[get_top].firstedge; edge; edge = edge->next) {  //遍历该顶点对应的边表
            k = edge->adjvex;
            if (!(--al_graph->adj_list[k].in)) {  //当前入度为零的顶点入栈
                vertex_stack.push(k);
            }
        }
    }
    if (count < al_graph->num_vertexes) {  //count小于顶点个数，存在环
        return false;
    }
    else {
        return true;
    }
}

对一个具有 n 个顶点 edge 条弧的 AOV 网来说，扫描顶点表，将入度为 0 的顶点入栈的时间复杂为 $O(n)$，而之后的 while 循环中，每个顶点进一次栈，出一次栈，入度减 1 的操作共执行了 edge 次，所以整个算法的时间复杂度为$O(n+edge)$。